286386577668298411128469151667598498812366
Създавайки сензация в математическата общност, само с 42 цифри група учени разкриват математическата загадка на така нареченото девето число на Дедекинд.
Математиците търсят тази стойност от 1991 г. Учените от Университета Падерборн и Католическия университет в град Льовен (KU Leuven), Белгия, стигат до точната последователност от числа с помощта на суперкомпютъра Noctua, разположен там. Резултатите ще бъдат представени през септември на Международния семинар за булеви функции и техните приложения (BFA) в Норвегия.
Това, което започва като проект за дипломната работа за магистърска степен на Ленарт Ван Хиртум (Lennart Van Hirtum) тогава студент по компютърни науки в KU Leuven и сега научен сътрудник в Университета в Падерборн, се превръща в огромен успех.
По-ранните числа в поредицата са открити от самия математик Ричард Дедекинд, когато той дефинира проблема през 1897 г., а по-късно - от двама велики ранни специалисти по компютърни науки - Рандолф Чърч (Randolph Church) и Морган Уорд (Morgan Ward).
„В продължение на 32 години изчисляването на D(9) бе открито предизвикателство и бе под въпрос дали изобщо ще бъде възможно да се изчисли това число“, разказва Ван Хиртум.
Предишното число в последователността на Дедекинд, 8-то число на Дедекинд, е намерено през 1991 г. с помощта на Cray 2, най-мощният суперкомпютър по това време.
„Струваше ни се възможно, че вече може да се изчисли 9-то число на голям суперкомпютър“, разказва Ван Хиртум, описвайки мотивацията за амбициозния проект, който той първоначално изпълнява съвместно с ръководителите на магистърската си дипломна работа в KU Льовен.
ЩО Е ТО ЧИСЛО НА ДЕДЕКИНД
Числото на Дедекинд е броят на монотонните булеви функции. Булевите функции се разглеждат от булевата алгебра, раздел от математическата логика. Тези функции приемат като вход n променливи, които могат да имат само две стойности: 0 или 1 (което съответства на "лъжа" или "истина"). Резултатът също може да бъде 0 или 1.
Монотонните булеви функции са функции, които ограничават логиката до два оператора - логическо "и" (AND, "&", конюнкция, "∧") и логическо "или" (OR, "|", дизюнкция, "∨"), без оператора "NOT". Така монотонните функции поредставляват подмножество от всички възможни булеви функции.
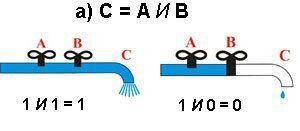 |
"1" тогава и само тогава, ако всички входове са "1" "0" ако и само ако поне един вход е "0" |
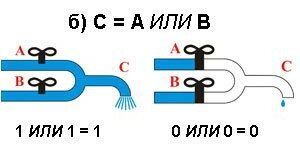 |
"1" ако и само ако поне един вход е "1" "0" тогава и само тогава, ако всички входове са "0" |
Кредит: elementy.ru
Колкото повече са променливите, толкова по-голямо е числото. Например, ако има 0 променливи, могат да съществуват само две функции: f = 0 и f = 1. За една променлива има три функции: f(x) = 0, f(x) = 1 и f(x) = x. За две променливи се добавят още три: втората променлива f(x,y) = y, както и логическото AND (x ∧ y) и логическото OR (x ∨ y). За три аргумента броят на функциите вече се увеличава до D(4) = 20, а за пет аргумента - до D(5) = 168.
В препринтите на arXiv.org математиците обясняват, че по същество може да си представите монотонна булева функция в две, три и безкрайно много измерения като игра с n-измерен куб. Според правилата на тази игра, балансирате куба на един ъгъл, след което оцветявате всеки от останалите ъгли в бяло или червено. При това никога не трябва да поставяте белия ъгъл върху червения. Така се получава нещо като вертикално пресичане на бялото и червеното. Целта на играта е да преброите колко различни конюнкции има.
Генериране на монотонни булеви функции
Монотонните булеви функции (събития) на n променливи са тези, които могат да бъдат конструирани само с помощта на операции И и ИЛИ (без НЕ). Един елементарен начин за конструиране и преброяване на тези функции е да се започне с функция от n=0 променливи, които могат да имат само постоянно състояние, или 0, или 1, без никакви логически операции. Така монотонните булеви функции с 0 променливи са:

За да конструираме монотонните функции на 1 променлива, можем просто да вземем всяка монотонна функция X от 0 променливи и да я присъединим към всяка друга монотонна функция Y от 0 променливи, така че X U Y = Y. Така можем да присъединим 0 или 1 към функция 0, но можем да присъединим само 1 към функцията 1. Това дава трите монотонни функции на 1 променлива

За да конструираме монотонните булеви функции на две променливи, ние повтаряме процеса, като разглеждаме всяка от функциите с една променлива X на свой ред и присъединяваме към нея всеки друг член Y от множеството с една променлива, така че X U Y = Y. Това дава шестте монотонни булеви функции на две променливи:

По същия начин, за да намерим монотонните булеви функции на три променливи, разглеждаме всяка монотонна функция с две променливи X и присъединяваме към нея всяка друга монотонна функция с две променливи Y, така че X U Y = Y. Това дава двадесетте монотонни булеви функции на три променливи:
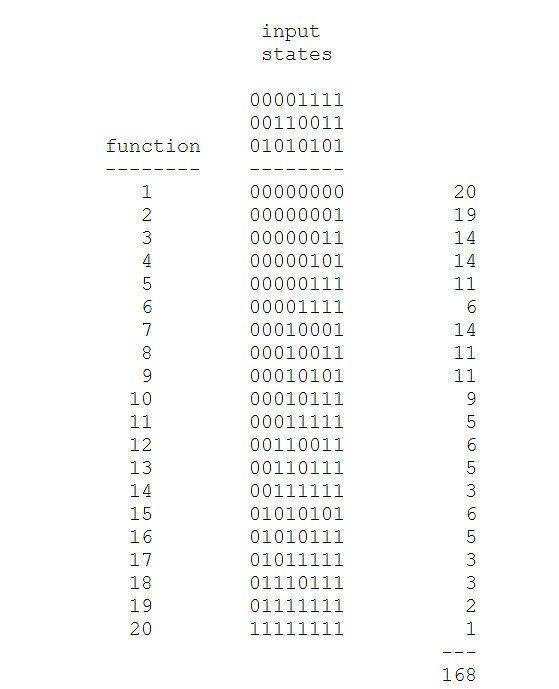
Числата в дясната колона показват за всяка от тези функции колко други в този списък я поемат. По този начин, ако преминем към следващия етап, ще произведем всичките 168 монотонни булеви функции с четири променливи.
Като цяло, булева функция от n променливи се състои от спецификацията на изходното състояние (0 или 1) за всяко от 2 n възможни входни състояния. Така има 2^(2 n ) възможни булеви функции на n променливи. Всяка от тези функции може да бъде представена с 2 n -битово двоично число F в диапазона от 0 до 2^(2 n ) – 1 и всяко входно състояние може да бъде представено с n-битово число I в диапазона от 0 до 2 n – 1. Дадена функция F е НЕмонотонна тогава и само тогава, когато за някои две входни състояния I 1 и I 2 имаме F(I 1 ) = 1 и F(I 2 ) = 0 и (I 1 OR I 2) = I 2 . Това просто изразява факта, че изходното състояние на монотонна функция не може да стане FALSE чрез просто задаване на един от входните компоненти TRUE, защото това би довело до функция за отрицание.

Това са първите 8 числа на Дедекинд.
ТАЗИ ЗАДАЧА Е РЕШЕНА ПРЕДИ 32 ГОДИНИ И МАТЕМАТИЦИТЕ СТИГАТ ДО ДЕВЕТАТА ЗАДЪНЕНА УЛИЦА
Първите няколко числа на Дедекинд били доста очевидни, след което започнали трудностите. Невъзможно е да се намери дедекиндово число за голям брой аргументи толкова просто, затова се използват или асимптотични решения, които определят интервала, в който попада желаната стойност, или точна формула, за чието използване са необходими значителни изчислителни ресурси. Формулата представлява сума, която се изразява от второто определение на числата на Дедекинд чрез антивериги, т.е. подмножества на подредено множество, в които (за разлика от веригата) всякакви двойки елементи са несравними. Числото на Дедекинд в този случай определя броя на елементите в решетката от антивериги в частично подреденото множество.
Резултатите от сумирането по тези формули се търсят с помощта на суперкомпютри. Последното вече намерено число на Дедекинд е осмото - D(8). Това 23-цифрено число е изчислено още през 1991 г. и са били необходими 200 часа, и то с един от най-мощните суперкомпютри по онова време - Cray-2. Оказва се, че това е 23-цифрено число.
През 2014 г. белгийските математици Патрик Де Каусмакер (Patrick De Causmaecker) и Стефан Де Ванемакер (Stefan De Wannemacker) от Католическия университет в Льовен предлагат друга версия на формулата, чрез която сумирането може да се използва за намиране на дедекиндови числа.
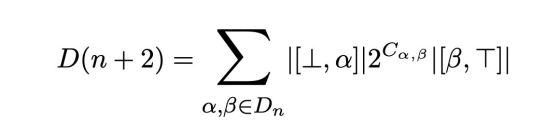
Сумиране за изчисляване на дедекиндните числа. Кредит: Lennart Van Hirtum et al / arXiv, 2023
Тази формула позволява да се разложи решетката на антиверигите на подрешетки в пространства с по-малка размерност. Шестизмерните подрешетки са били достатъчни, за да се изчисли на суперкомпютър D(8) и да се потвърди вече известната стойност, но за изчисляване на следващото число компютърната мощ не бе достатъчна.
Сега учените са взели тази формула и са я адаптирали към възможностите на съвременните компютри. След три месеца изчисления със суперкомпютърния клъстер Noctua 2 те успяват да получат деветото число на Дедекинд.
И ето как изглежда то: 286386577668298411128469151667598498812366.
Справка: A computation of D(9) using FPGA Supercomputing
Lennart Van Hirtum, Patrick De Causmaecker, Jens Goemaere, Tobias Kenter, Heinrich Riebler, Michael Lass and Christian Plessl https://arxiv.org/pdf/2304.03039.pdf
Източници:
Ninth Dedekind number discovered: Scientists solve long-known problem in mathematics, Universität Paderborn
Dedekind's Problem, Generating the Monotone Boolean Functions, mathpages